Question

A bag contains some number of marbles. It is known that 20 of them are red. When 15 marbles are drawn, without replacement, we get 6 red. Assuming E(X)=6 red, what is the total number of marbles in the bag?

Answer 1

The total number of marbles in the bag is 50.

Explanation:

Here, we have n trials, without replacement. So the hypergeometric distribution is used.

The mean of the hypergeometric distribution is:

`E(X) = (n*k)/(N)`

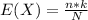
In which n is the number of items in the sample, k is the number of items in the population that are classified a success and N is the size of the population.

15 marbles are drawn:

This means that
`n = 15`

A bag contains some number of marbles. It is known that 20 of them are red.

This means that
`k = 20`, since a success is drawing a red marble.

Assuming E(X)=6 red, what is the total number of marbles in the bag?

We have to find N when
`E(X) = 6`

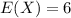
So

`E(X) = (n*k)/(N)`

`6 = (15*20)/(N)`

`6N = 300`

`N = (300)/(6)`

`N = 50`

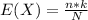
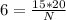
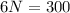
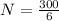
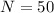
The total number of marbles in the bag is 50.