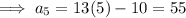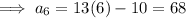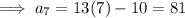Answer:
B) 55, 68, 81
Explanation:
Given sequence: 3, 16, 29, 42
To determine if the sequence is arithmetic or geometric, work out the difference in the terms.
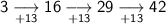
This sequence adds 13 each time, so as the common difference is constant, it is an arithmetic sequence. To find the next term in the sequence, simply add 13 to the last term:
42 + 13 = 55
55 + 13 = 68
68 + 13 = 81
Therefore, the next three terms in the given sequence are 55, 68, 81
To solve this using the general form of an arithmetic sequence:
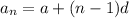
where:
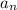 is the nth term
is the nth term- a is the first term
- d is the common difference between terms
Given:
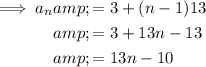
Therefore, the next 3 terms in the sequence are: