Question

you secure a mortgage to buy a house with a loan of $140,000 at 8.5% for 20 years. answer the following questions about that loan for the first two months of payments: a) what is the monthly payment? b)how much of the monthly payment goes toward interest when you submit your first payment? c)what is your balance after the first payment? d) how much of the monthly payment goes toward interest when you submit your second payment? e) what is your balance after the second payment?

Answer 1

• monthly payment $1214.95
• 1st month's interest $991.67
• balance after 1st payment $139,776.72
• 2nd month's interest $990.09
• balance after 2nd payment $139,551.86

Explanation:

The monthly interest rate is ...

`(8\%)/(12)=0.00708\overline{3}`

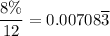
a) The monthly payment is given by the amortization formula:

A = Pr/(1 -(1+r)^-n)

where r is the monthly interest rate on a loan of amount P for n months.

A = $140,000(0.0070833)/(1 -(1.0070833^-240)) = $1214.95

The monthly payment is $1214.95.

__

b) The amount to interest is the product of the remaining principal and the monthly interest rate.

first month's interest = $140,000·0.0070833 = $991.67

__

c) The balance after the first payment is ...

new balance = $140,000 +991.67 -1214.95 = $139,776.72

__

d) The amount to interest for the second payment is computed the same way:

second month's interest = $139,776.72·0.00708333 = $990.09

__

e) The balance after the second payment is computed the same way:

new balance = $139,776.72 +990.09 -1214.95 = $139,551.86