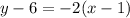Answer:
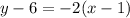
Explanation:
Given; The graph above
Required: Equation of line AB (in point slope form)
First, we need to determine the slope of the graph;
From the graph; we can observe that when y = 6, x = 1 and when y = 2, x = 3
Such that
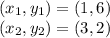
The slope of a line is define as thus;

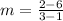
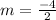
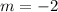
Considering only point
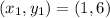 ; The slope is define as thus
; The slope is define as thus

Substitute
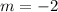 and
and
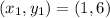

Multiply both sides by x - 1
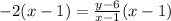
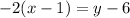
Rearrange
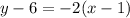
Hence, the equation of the line is a point slope form is