Answer:
(a) The probability that more than 180 will take your free sample is 0.1056.
(b) The probability that fewer than 200 will take your free sample is 0.9997.
(c) The probability that a customer will take a free sample and buy the product is 0.2184.
(d) The probability that between 60 and 80 customers will take the free sample and buy the product is 0.8005.
Explanation:
We are given that about 56% of all customers will take free samples. Furthermore, of those who take the free samples, about 39% will buy what they have sampled.
The day you were offering free samples, 303 customers passed by your counter.
Firstly, we will check that it is appropriate to use the normal approximation to the binomial, that is;
Is np > 5 and n(1-p) > 5
In our question, n = sample of customers = 303
p = probability that customers will take free sample = 56%
So, np =
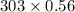 = 169.68 > 5
= 169.68 > 5
n(1-p) =
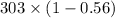 = 133.32 > 5
= 133.32 > 5
Since, both conditions are satisfied so it is appropriate to use the normal approximation to the binomial.
Now, mean of the normal distribution is given by;
Mean,
 =
=
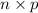 = 169.68
= 169.68
Also, the standard deviation of the normal distribution is given by;
Standard deviation,
 =
=
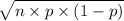
=
 = 8.64
= 8.64
Let X = Number of people who will take your free sample
The z score probability distribution for normal distribution is given by;
Z =
 ~ N(0,1)
~ N(0,1)
(a) The probability that more than 180 will take your free sample is given by = P(X > 180) = P(X > 180.5) {Using continuity correction}
P(X > 180.5) = P(
 >
>
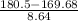 ) = P(Z > 1.25) = 1 - P(Z < 1.25)
) = P(Z > 1.25) = 1 - P(Z < 1.25)
= 1 - 0.8944 = 0.1056
(b) The probability that fewer than 200 will take your free sample is given by = P(X < 200) = P(X < 199.5) {Using continuity correction}
P(X < 199.5) = P(
 <
<
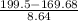 ) = P(Z < 3.45) = 0.9997
) = P(Z < 3.45) = 0.9997
(c) We are given in the question that of those who take the free samples, about 39% will buy what they have sampled, this means that we have;
P(Buy the product / taken a free sample) = 0.39
So, Probability(customer will take a free sample and buy the product) = P(customer take a free sample)
 P(Buy the product / taken a free sample)
P(Buy the product / taken a free sample)
= 0.56
 0.39 = 0.2184
0.39 = 0.2184
(d) Now our mean and standard deviation will get changed because the probability of success now is p = 0.2184 but n is same as 303.
So, Mean,
 =
=
 =
=
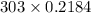 = 66.18
= 66.18
Standard deviation,
 =
=
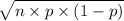
=
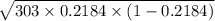 = 7.192
= 7.192
Now, the probability that between 60 and 80 customers will take the free sample and buy the product is given by = P(60 < X < 80) = P(59.5 < X < 80.5) {Using continuity correction}
P(59.5 < X < 80.5) = P(X < 80.5) - P(X
 59.5)
59.5)
P(X < 80.5) = P(
 <
<
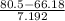 ) = P(Z < 1.99) = 0.9767
) = P(Z < 1.99) = 0.9767
P(X
 59.5) = P(
59.5) = P(


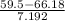 ) = P(Z
) = P(Z
 -0.93) = 1 - P(Z < 0.93)
-0.93) = 1 - P(Z < 0.93)
= 1 - 0.8238 = 0.1762
Therefore, P(59.5 < X < 80.5) = 0.9767- 0.1762 = 0.8005.