Answer:
(a, b, c) = (12, 2, 11)
Explanation:
We assume you want to simplify ...
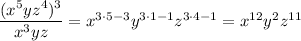
Compared to (x^a)(y^b)(z^c), we find that ...
(a, b, c) = (12, 2, 11)
_____
The applicable rules of exponents are ...
(a^b)^c = a^(bc)
(ab)^c = (a^c)(b^c)
(a^b)/(a^c) = a^(b-c)