Answer:
 , I hope this is right. Im kind of new to integral calculus
, I hope this is right. Im kind of new to integral calculus
Explanation:
You essentially want to split this integral into two parts, because its a piecewise function. The conditions on the right side basically say for when x is less than and when x is greater than 0. So, we should split this integral at 0.
The first function says that -pi is less than 0, so change the upper boundary to 0. This make the definite integral bounded at -pi to 0. But now, we have to take the anti derivative of 2x^4 using the reverse power rule. Add one to the power, then divide by the new power. So the new function is
 defined at lower boundary -pi and upper boundary of 0. Use the fundamental theorem of calculus to solve the integral. You get
defined at lower boundary -pi and upper boundary of 0. Use the fundamental theorem of calculus to solve the integral. You get
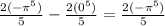 . You want to add the 2nd integral to this, so lets go solve that.
. You want to add the 2nd integral to this, so lets go solve that.
Now for this integral, we have the conditions that pi is greater than 0. So 0 will be in the lower boundary this time and pi will be in the upper. Basically apply the same thing from the first integral. Do anti derivative and use fund. theorem of calculus. the anti-derivative of sinx is -cosx. You can take this 9 out because its a constant that is scaling -cosx. So now 9 is on the outside of the integral and you have the definite integral of -cosx with the boundaries of 0 and pi. Plug in pi to get -1, then multiply that by the negative sign to get postive 1. Now let's plug in the lower boundary, 0. Cosine of 0 is 1, then we are multiplying by the negative sign to get -1. Subtract 1 and -1 to get postive 2. Finally multiply that by the 9 from before to get 18
Final Answer finally:
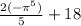
OH, do not forget the C. This took me 30 minutes of constant typing so hopefully Im right