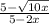Answer:
The equivalent fraction is:
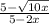
which agrees with the second answer in the list of options
Explanation:
Recall that in order to rationalize a denominator of this type (remove the square roots), we need to multiply numerator and denominator of the fraction we have by the conjugate of the binomial. That is, multiply top and bottom of the fraction by the expression:
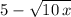
Therefore we have:
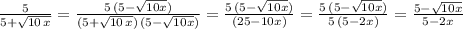
Then this is the equivalent rationalized expression: