Answer:
3u-2v =
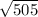
5u-v =
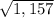
2u-3v =
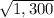
u+4v =
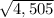
Explanation:
I just started by doing the results for each of the operations given.
3u-2v:
3u = (-9, 24) 2v = (-28, 12)
Do the operation of 3u-2v and you get a resultant vector of (19, 12).
You calculate this by doing the square root of 19^2 + 12^2, which is the square root of 505.
5u-v:
5u = (-15, 40) v = (-14, 6)
Do the operation of 5u-v and you get a resultant vector of (-1, 34).
You calculate this by doing the square root of (-1)^2 + 34^2, which is the square root of 1,157.
2u-3v:
2u = (-6, 16) 3v = (-42, 18)
Do the operation of 2u-3v and you get a resultant vector of (36, -2).
You calculate this by doing the square root of 36^2 + (-2)^2, which is the square root of 1,300.
3u+2v:
3u = (-9, 24) 2v = (-28, 12)
Do the operation of 3u+2v and you get a resultant vector of (-37, 36).
You calculate this by doing the square root of (-37)^2 + 36^2, which is the square root of 2,665. This is not a given tile, so we can just ignore this one.
u+4v:
u = (-3, 8) 4v = (-56, 24)
Do the operation of u+4v and you get a resultant vector of (-59, 32).
You calculate this by doing the square root of (-59)^2 + 32^2, which is the square root of 4,505.
Since this is a given tile, I didn't do 7u-2v, but you would use the same methodology.