Question

If an altitude is drawn from the right angle of a right triangle to its hypotenuse, the two segments formed on the hypotenuse are 11.25 cm and 5 cm, then what is the length of the altitude?

Answer 1

the length of the altitude is 7.5 cm

Explanation:

In a Δ ABC,
`\overline {BC}` is the altitude

If an altitude is drawn to the hypotenuse of the right angle triangle as shown in the image attached below; Then:

`(AD)^2 = AD*AC \\ \\ x^2 = 5*11.25 \\ \\ x^2 = 81.25 \\ \\ x = √(81.25) \\ \\ x= 9.01`

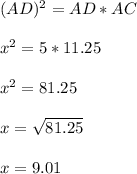
NOW;

`(BC)^2 = DC*AC \\ \\ z^2 = 11.25 *16.25 \\ \\z^2 = 182.8125 \\ \\ z= √(182.8125) \\ \\ z= 13.52`

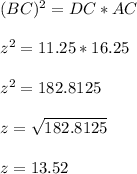
Finally; the altitude which is
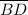`\overline {BD}` is calculated as:

`(BD)^2 = AD*DC \\ \\ y^2 = 5*11.25 \\ \\ y^2 = 56.25 \\ \\ y = √(56.25) \\ \\ y= 7.5`

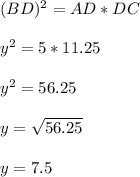
Thus; the length of the altitude is 7.5 cm