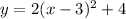Question

I need help this exact minute
no fake answers, seriously no.

Answer 1

h is the horizontal translation

k is the vertical translation

a is the stretch parallel to the y-axis

Explanation:

Parent equation:
`y=x^2`

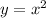
Translate
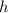`h` units right:
`y=(x-h)^2`

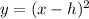
(if
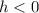`h < 0`, then the translation is
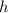`h` units left)

Stretched parallel to the y-axis by a factor of
`a`:
`y=a(x-h)^2`

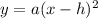
(if
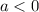`a < 0`, the graph is also reflected in the x-axis)

Translated k units up:
`y=a(x-h)^2+k`

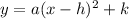
(if
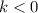`k < 0` then the translation is k units down)

Example attached for
`y=2(x-3)^2+4`