Answer:
The slope of the line is 3 and the y-intercept is (3/2) three-halves.
Explanation:
The data provided is:
X Y
-1.0 -1.5
-0.5 0.0
0.0 1.5
0.5 3.0
The slope of the linear function is denoted by, b and the intercept is denoted by, a.
The formula to compute the slope and intercept are:
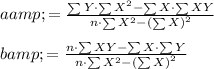
Compute the values required in Excel.
Compute the slope and intercept as follows:
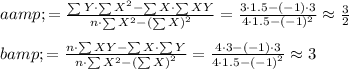
Thus, the slope of the line is 3 and the y-intercept is (3/2) three-halves.