Answer:
For k = 1:
=NEGBINOMDIST(0, 1, 0.666) = 0.6660
For k = 2:
=NEGBINOMDIST(1, 1, 0.666) = 0.2224
For k = 3:
=NEGBINOMDIST(2, 1, 0.666) = 0.0743
For k = 4:
=NEGBINOMDIST(3, 1, 0.666) = 0.0248
For k = 5:
=NEGBINOMDIST(4, 1, 0.666) = 0.0083
For k = 6:
=NEGBINOMDIST(5, 1, 0.666) = 0.0028
Explanation:
The probability of obtaining a defective 10-year old widget is 66.6%
p = 66.6% = 0.666
The probability of obtaining a non-defective 10-year old widget is
q = 1 - 0.666 = 0.334
The random variable will be the number of items that must be tested before finding the first defective 10-year old widget.
The geometric distribution is given by
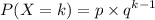
Solving manually:
For k = 1:
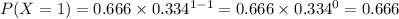
For k = 2:
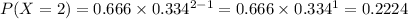
For k = 3:

For k = 4:
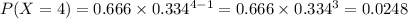
For k = 5:

For k = 6:
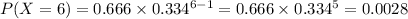
Using Excel function:
NEGBINOMDIST(number_f, number_s, probability_s)
Where
number_f = k - 1 failures
number_s = no. of successes
probability_s = the probability of success
For the geometric distribution, let number_s = 1
For k = 1:
=NEGBINOMDIST(0, 1, 0.666) = 0.6660
For k = 2:
=NEGBINOMDIST(1, 1, 0.666) = 0.2224
For k = 3:
=NEGBINOMDIST(2, 1, 0.666) = 0.0743
For k = 4:
=NEGBINOMDIST(3, 1, 0.666) = 0.0248
For k = 5:
=NEGBINOMDIST(4, 1, 0.666) = 0.0083
For k = 6:
=NEGBINOMDIST(5, 1, 0.666) = 0.0028
As you can notice solving manually and using Excel yields the same results.