Answer:
![\sqrt[3]{3}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/iki7lm4dww0iksbkrp22a5afiv8jk1hogs.png)
Explanation:
Our expression is:
![(1)/(3) \sqrt[3]{81}](https://img.qammunity.org/2021/formulas/mathematics/high-school/y8j3l1hbww7xei7pdw6ujshzkv1k11e2dd.png) .
.
Let's focus on the cube root of 81 first. What's the prime factorisation of 81? It's simply: 3 * 3 * 3 * 3, or
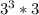 . Put this in for 81:
. Put this in for 81:
![\sqrt[3]{81} =\sqrt[3]{3^3*3}=\sqrt[3]{3^3} *\sqrt[3]{3}](https://img.qammunity.org/2021/formulas/mathematics/high-school/9u4ka2scqcjb9a6fi0623gzsxop9cmtax5.png)
We know that the cube root of 3 cubed will cancel out to become 3, but the cube root of 3 cannot be further simplified, so we keep that. Our outcome is then:
![\sqrt[3]{3^3} *\sqrt[3]{3}=3\sqrt[3]{3}](https://img.qammunity.org/2021/formulas/mathematics/high-school/12g6pqzsrd0viq27qqspt6j9z66mjldm9k.png)
Now, let's multiply this by 1/3, as shown in the original problem:
![(1)/(3)* 3\sqrt[3]{3}=\sqrt[3]{3}](https://img.qammunity.org/2021/formulas/mathematics/high-school/6nso77zeiok1b24jf3z2as4kzwvqz1se2c.png)
Thus, the answer is
![\sqrt[3]{3}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/iki7lm4dww0iksbkrp22a5afiv8jk1hogs.png) .
.
~ an aesthetics lover