Answer:
Explanation:
Given:
Type of Flowers = 5
To choose = 4
Required
Number of ways 4 can be chosen
The first flower can be chosen in 5 ways
The second flower can be chosen in 4 ways
The third flower can be chosen in 3 ways
The fourth flower can be chosen in 2 ways
Total Number of Selection = 5 * 4 * 3 * 2
Total Number of Selection = 120 ways;
Alternatively, this can be solved using concept of Permutation;
Given that 4 flowers to be chosen from 5,
then n = 5 and r = 4
Such that

Substitute 5 for n and 4 for r
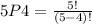
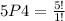
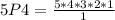
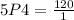
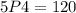
Hence, the number of ways the florist can chose 4 flowers from 5 is 120 ways