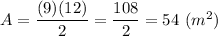Answer:
54m²
Explanation:
METHOD 1:
You can use the Heron's formula:
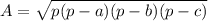
where
p - half of perimeter
a, b, c - lengths of sides
We have

Calculate:
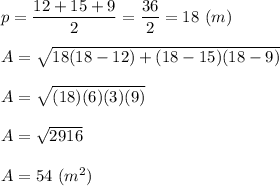
METHOD 2:
Let's check that it is not a right triangle.
If the sum of the squares of the two shorter sides is equal to the square of the longest side, then this triangle is rectangular.
We have
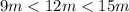
Check:

This is a right trianglr wherew 9m and 12m are legs and 15m is a hypotenuse.
The formula of an area of a right triangle is:
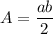
a, b - legs
Substitute: