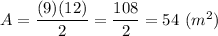Question

ANSWER ASAP!! Find the area of a triangle with legs that are: 12 m, 15 m, and 9 m.

Answer 1

54m²

Explanation:

METHOD 1:

You can use the Heron's formula:

`A=√(p(p-a)(p-b)(p-c))`

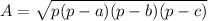
where

p - half of perimeter

a, b, c - lengths of sides

We have

`a=12m;\ b=15m;\ c=9m`

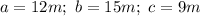
Calculate:

`p=(12+15+9)/(2)=(36)/(2)=18\ (m)\\\\A=√(18(18-12)+(18-15)(18-9))\\\\A=√((18)(6)(3)(9))\\\\A=√(2916)\\\\A=54\ (m^2)`

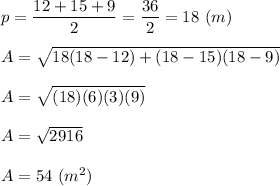
METHOD 2:

Let's check that it is not a right triangle.

If the sum of the squares of the two shorter sides is equal to the square of the longest side, then this triangle is rectangular.

We have

`9m < 12m<15m`

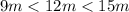
Check:

`9^2+12^2=81+144=225\\15^2=225`

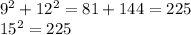
This is a right trianglr wherew 9m and 12m are legs and 15m is a hypotenuse.

The formula of an area of a right triangle is:

`A=(ab)/(2)`

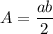
a, b - legs

Substitute:

`A=((9)(12))/(2)=(108)/(2)=54\ (m^2)`