Question

Find the area of a triangle bounded by the y-axis, the line f(x)=9−2/3x, and the line perpendicular to f(x) that passes through the origin. Area =

Answer 1

The area of the triangle is 18.70 sq.units.

Explanation:

It is provided that a triangle is bounded by the y-axis, the line
`f(x)=y=9-(2)/(3)x`.

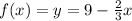The slope of the line is:
`m_(1)=-(2)/(3)`

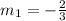
A perpendicular line passes through the origin to the line f (x).

The slope of this perpendicular line is:
`m_(2)=-(1)/(m_(1))=(3)/(2)`

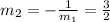
The equation of perpendicular line passing through origin is:

`y=(3)/(2)x`

Compute the intersecting point between the lines as follows:

`y=9-(2)/(3)x\\\\(3)/(2)x=9-(2)/(3)x\\\\(3)/(2)x+(2)/(3)x=9\\\\(13)/(6)x=9\\\\x=(54)/(13)`

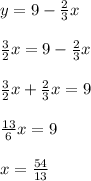
The value of y is:

`y=(3)/(2)x=(3)/(2)*(54)/(13)=(81)/(13)`

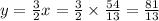
The intersecting point is
`((54)/(13),\ (81)/(13))`.

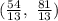The y-intercept of the line f (x) is, 9, i.e. the point is (0, 9).

So, the triangle is bounded by the points:

(0, 0), (0, 9) and
`((54)/(13),\ (81)/(13))`

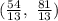
Consider the diagram attached.

Compute the area of the triangle as follows:

`\text{Area}=(1)/(2)* 9* (54)/(13)=18.69231\approx 18.70`

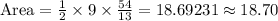
Thus, the area of the triangle is 18.70 sq.units.