Answer:
(a)123 km/hr
(b)39 degrees
Explanation:
Plane X with an average speed of 50km/hr travels for 2 hours from P (Kano Airport) to point Q in the diagram.
Distance = Speed X Time
Therefore: PQ =50km/hr X 2 hr =100 km
It moves from Point Q at 9.00 am and arrives at the airstrip A by 11.30am.
Distance, QA=50km/hr X 2.5 hr =125 km
Using alternate angles in the diagram:
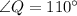
(a)First, we calculate the distance traveled, PA by plane Y.
Using Cosine rule
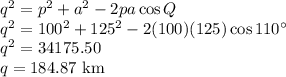
SInce aeroplane Y leaves kano airport at 10.00am and arrives at 11.30am
Time taken =1.5 hour
Therefore:
Average Speed of Y
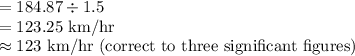
(b)Flight Direction of Y
Using Law of Sines
![(p)/(\sin P) =(q)/(\sin Q)\\(125)/(\sin P) =(184.87)/(\sin 110)\\123 * \sin P=125 * \sin 110\\\sin P=(125 * \sin 110) / 184.87\\P=\arcsin [(125 * \sin 110) / 184.87]\\P=39^\circ $ (to the nearest degree)](https://img.qammunity.org/2021/formulas/mathematics/college/6thkrk5nech4uhlawbaa9kt3yth5wqqsd9.png)
The direction of flight Y to the nearest degree is 39 degrees.