Answer:
(8, 15, 17); (9, 12, 15); (15; 20; 25)
Explanation:
If
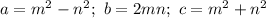
for m > n, then a, b, c make a Pythagorean triplet.
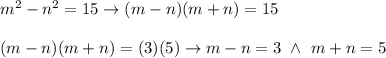
We have the system of equations:

Substitute to the second equation:
![4+n=5\qquad\text{subtract 4 from both sides}\\\boxed{n=1]()
Therefore we have:

 it's impossible, because 15 is not an even number.
it's impossible, because 15 is not an even number.
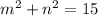
Let's consider all possible sums of two numbers resulting in 15.
We will check which of the numbers are perfect squares.
1 + 14
2 + 13
3 + 12
4 + 11
5 + 10
6 + 9
7 + 8
(Bold not perfect squares)
There are no two perfect squares among the listed pairs of numbers.
Other:
15, 112, 113
We know the Egyptian triangle with sides of length 3, 4, 5.
By modifying this Pythagorean triplet by multiplying by 3 we get:
(3)(3) = 9; (3)(4) = 12; (3)(5) = 15
By modifying this Pythagorean triplet by multiplying by 5 we get:
(5)(3) = 15; (5)(4) = 20; (5)(5) = 25