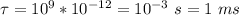Question

In an RC-circuit, a resistance of R=1.0 "Giga Ohms" is connected to an air-filled circular-parallel-plate capacitor of diameter 12.0 mm with a separation distance of 1.0 mm. What is the time constant of the system?

Answer 1

`\tau = 1\ ms`

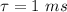
Step-by-step explanation:

First we need to find the capacitance of the capacitor.

The capacitance is given by:

`C = \epsilon_0 * area / distance`

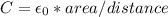
Where
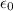`\epsilon_0` is the air permittivity, which is approximately 8.85 * 10^(-12)

The radius is 12/2 = 6 mm = 0.006 m, so the area of the capacitor is:

`Area = \pi * radius^(2)\\Area = \pi * 0.006^2\\Area = 113.1 * 10^(-6)\ m^2`

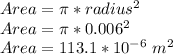
So the capacitance is:

`C = (8.85 * 10^(-12) * 113.1 * 10^(-6))/(0.001)`

`C = 10^(-12)\ F = 1\ pF`

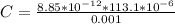
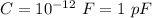
The time constant of a rc-circuit is given by:

`\tau = RC`

So we have that:

`\tau = 10^(9) * 10^(-12) = 10^(-3)\ s = 1\ ms`