Question

Please someone help me, i need thier solve please my teacher told me to solve them ​

Answer 1

A. Domain : (-∞, ∞)

B. Function is increasing in the interval (-2, 0) and (2, ∞)

Decreasing in the interval of (-∞, -2) and (0, 2).

Explanation:

A. Given function is, y = |2x - 1|

This function is the transformed form of the parent function, y = |x|

Domain of the parent function is x is a set of real numbers

Therefore, domain of the transformed function will be the same as the domain of the parent function.

Domain of the function = x is a real number

B. Given function is f(x) =
`(x^2-4) ^{(2)/(3) }`

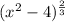
Domain of the function : (-∞, ∞)

Critical points of the function are,

⇒ x = 0, ±2

Now we find the three intervals where we have to check the function to be increasing or decreasing.

(-∞ -2), (-2, 0), (0, 2), (2, ∞)

Derivative of the function f(x),

f'(x) =
`\frac{4x}{3(x^2-4)^{(1)/(3) } }`

Here, f'(x) < 0 for (-∞, -2)

f'(x) > 0 for (-2, 0)

f'(x) < 0 for (0, 2)

f'(x) > 0 for (2, ∞)

Therefore, given function is increasing in the interval (-2, 0) and (2, ∞)

And it's decreasing in the interval of (-∞, -2), and (0, 2).