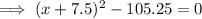Question

Let ​ x² + 15x = 49 .​ What values make an equivalent number sentence after completing the square? Enter your answers in the boxes.

x² + 15x + ​= ​ [ ]

Answer 1

Explanation:

15/2 = 7.5 and (7.5)^2 = 56.25 so

x^2 + 15x + 56.25 = 49 + 56.25

x^2 + 15x + 56.25 = 105.25.

Answer 2

`x^2+15x+\boxed{(225)/(4)}=\boxed{(421)/(4)}`

`x^2+15x+\boxed{56.25}=\boxed{105.25}`

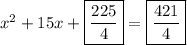
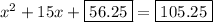
Explanation:

General form of a quadratic equation:
`ax^2+bx+c`

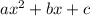
When completing the square, first add the number that is the square of half of
`b`.

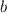Given equation:
`x^2+15x=49`

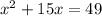
Therefore,
`b=15`

`\implies \left((b)/(2)\right)^2=\left((15)/(2)\right)^2=(225)/(4)`

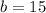
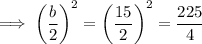
So we need to add 225/4 to both sides of the equation:

`\implies x^2+15x+(225)/(4)=49+(225)/(4)`

`\implies x^2+15x+\boxed{(225)/(4)}=\boxed{(421)/(4)}`

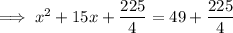
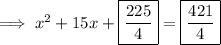
In decimal form:

`\implies x^2+15x+\boxed{56.25}=\boxed{105.25}`

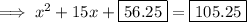
To finish completing the square,

factor the left side of the equation:

`\implies \left(x+(15)/(2)\right)^2=(421)/(4)`

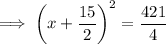
Finally, subtract 421/4 from both sides:

`\implies \left(x+(15)/(2)\right)^2-(421)/(4)=0`

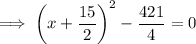
In decimal form:

`\implies (x+7.5)^2-105.25=0`