Answer:
The solution is
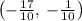 .
.
Explanation:
An inequality is a mathematical relationship between two expressions and is represented using one of the following:
- ≤, "less than or equal to"
- <, "less than"
- >, "greater than"
- ≥, "greater than or equal to"
To find the solution of the inequality
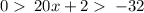 you must:
you must:
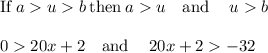
First, solve
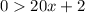
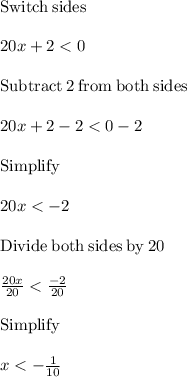
Next, solve
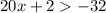
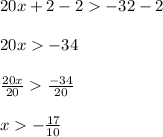
Finally, combine the intervals
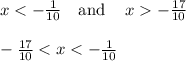
The interval notation is
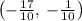 and the graph is:
and the graph is: