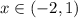Answer:
Explanation:
We are given that a function
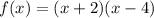
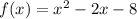
Differentiate w.r.t x
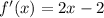
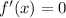
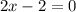

Therefore, intervals
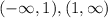
Interval :
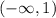
x=0
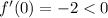
Decreasing function.
Interval:
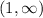
Substitute x=2
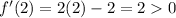
Function increasing.
From given graph we can see that function is negative for the values of x
-2<x<4
Hence, the graph is negative and decreasing for the values of x