Question

What is the perimeter of ABCDE, rounded to the nearest whole number?

Answer 1

option B -> 23 units

Explanation:

To solve this question we need to find the length of each side, and we can do this finding the distance between the pair of points that make a side, using the formula:

`dist = \sqrt{(x_1 - x_2)^(2) + (y_1 - y_2)^(2) }`

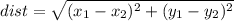
Where the points are
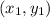`(x_1, y_1)` and
`(x_2, y_2)`.

So, using the points A = (-4, -2), B = (-1, 2), C = (2, 2), D = (5, -1) and E = (2, -4), we have that:

`AB = \sqrt{(-4 - (-1))^(2) + (-2 - 2)^(2) } = 5`

`BC = \sqrt{(-1 - 2)^(2) + (2 - 2)^(2) } = 3`

`CD = \sqrt{(2 - 5)^(2) + (2 - (-1))^(2) } = 4.2426`

`DE = \sqrt{(5 - 2)^(2) + (-1 - (-4))^(2) } = 4.2426`

`EA = \sqrt{(2 - (-4))^(2) + (-4 - (-2))^(2) } = 6.3246`

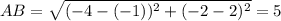
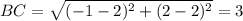
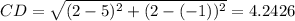
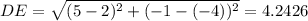
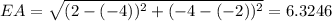
So the perimeter of ABCDE is:

`P(ABCDE) = AB + BC + CD + DE + EA`

`P(ABCDE) = 5 + 3 + 4.2426 + 4.2426 + 6.3246 = 22.8098`

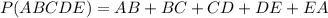
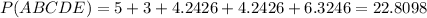
Rounding to nearest whole number we have:

`P(ABCDE) = 23`

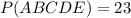
So the answer is the option B.