Question

When rewriting in the form y=a(x-h)+k, by completing the square, the relation y=-x*2+6x+12 becomes:

Answer 1

Explanation:

you can complete the square or use a calculator online that does it for you.

the equation is in the for y = a(x-h)^2 + k

it should be y = (x + 3)^2 + 3

Answer 2

The correct answer is
`y = - (x - 3)^(2) +21`.

Explanation:

To solve this equation (y =
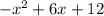`-x^(2) +6x + 12`), we want to first complete the square. To do this, we want to add a -9 to the expression in order to achieve
`y = -x^(2) +6x - 9 + 12`.

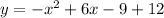Then, you want to add the -9 to the other side of the equation to get
`y - 9 = -x^(2) + 6x - 9 + 12`.

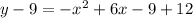Then, we factor out the negative sign from the right side of the equation. This is a negative 1 that can therefore make the polynomial easier to factor. This leaves us with
`y - 9 = -(x^(2) -6x+9) + 12`.

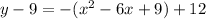Now, we use an identity in algebra that is difference of two squares identity. This says that
`a^(2) -2ab +b^(2) =(a-b)^(2)`.

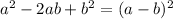So, we will then factor the trinomial -
`x^(2) -6x+9` to get
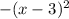`-(x-3)^(2)`. Our new and updated equation is
`y-9 = -(x-3)^(2) +12`.

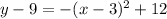Now, we move the constant of -9 to the right side of the equation. This just means we are going to add this to 12. This gives us
`y = -(x-3)^(2) +21`.

This is our final equation.