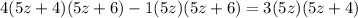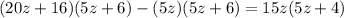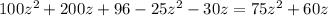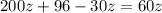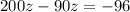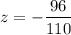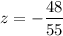Answer:
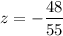
It has one solution.
Explanation:

Once we have fractions we already know the values when the equation is not true. I'm talking about division when the denominator is 0. It is undefined.
The values for
 are:
are:
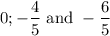
Now let's find
 . First, we have to find the least common multiplier:
. First, we have to find the least common multiplier:
In this case:
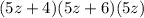

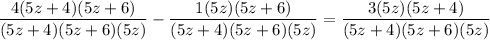
I will not proceed in the way above because it would take some time to type, instead, multiply
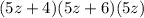 both sides.
both sides.