Question

A recipe submitted to a magazine by one of its subscribers’ states that the mean baking time for a cheesecake is 55 minutes. A test kitchen preparing the recipe before it is published in the magazine makes the cheesecake 10 times at different times of the day in different ovens. The following baking times (in minutes) are observed.

54 55 58 59 59 60 61 61 62 65
Assume that the baking times belong to a normal population. Test the null hypothesis that the mean baking time is 55 minutes against the alternative hypothesis μ > 55. Use α = .05.

Answer 1

`t=(59.4-55)/((3.239)/(√(10)))=4.296`

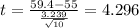
The degrees of freedom are given by:

`df=n-1=10-1=9`

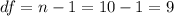
The p value for this case is given by:

`p_v =P(t_((9))>4.296)=0.001`

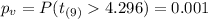
And for this case the p value is lower than the significance level so we have enough evidence to reject the null hypothesis and then we can conclude that true mean is higher than 55.

Explanation:

Information given

We have the following data: 54 55 58 59 59 60 61 61 62 65

The sample mean and deviation can be calculated with the following formulas:

`\bar X = (\sum_(i=1)^n X_i)/(n)`

`s=\sqrt{(\sum_(i=1)^n (X-i -\bar x)^2)/(n-1)}`

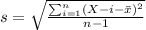
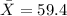`\bar X=59.4` represent the sample mean

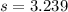`s=3.239` represent the sample standard deviation

`n=10` sample size

`\alpha=0.05` represent the significance level

t would represent the statistic

`p_v` represent the p value

System of hypothesis

We want to test if the true mean is higher than 55, the system of hypothesis would be:

Null hypothesis:
`\mu \leq 55`

Alternative hypothesis:
`\mu > 55`

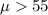
Replacing the info given we got:

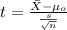`t=(\bar X-\mu_o)/((s)/(√(n)))` (1)

And replacing the info given we got:

`t=(59.4-55)/((3.239)/(√(10)))=4.296`

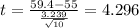
The degrees of freedom are given by:

`df=n-1=10-1=9`

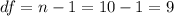
The p value for this case is given by:

`p_v =P(t_((9))>4.296)=0.001`

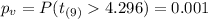
And for this case the p value is lower than the significance level so we have enough evidence to reject the null hypothesis and then we can conclude that true mean is higher than 55