Question

A researcher classifies firefighters according to whether their gloves fit well or poorly and by gender. They want to know if there is a difference in the proportion of poorly fitted gloves and gender. At alpha = 0.01, use the chi-square test to determine if there is a difference in the population proportion of glove fitness for the two genders.

Observed data Males Females Total
Gloves fit poorly 132 20 152
Gloves fit well 415 19 434
Total 547 39 586
Expected data Males Females Total
Gloves fit poorly
Gloves fit well
Total

Answer 1

The Chi - Square Test Statistics is 13.98

p-value = 0.0002

CONCLUSION: Since the p-value is less than the level of significance ; (i.e p-value < ∝) we reject the null hypothesis and accept the alternative hypothesis.

Thus; there is a difference in the population proportion of glove fitness for the two genders.

Explanation:

From the information given ; the structure of the table can be well represented as follows;

Observed data Males Females Total

Gloves fit poorly 132 20 152

Gloves fit well 415 19 434

Total 547 39 586

Expected data Males Females Total

Gloves fit poorly

Gloves fit well

Total

The objective of this question is to use the chi-square test to determine if there is a difference in the population proportion of glove fitness for the two genders.

We call represent the hypothesis as follows:

The null hypothesis:
`H_o:` states that there is no difference in the population proportion of glove fitness for the two genders.

The alternative hypothesis:
`H_a` states that there is difference in the population proportion of glove fitness for the two genders.

The expected frequency of a particular cell can be calculated by multiplying the sum of the rows and columns together, then dividing it by the Total sum

For row 1 column 1 (gloves fit poorly (male) ; we have:

`= (547*152)/(586) =141.884\\`

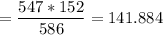
For row 2 column 1 (gloves fit well(male) ; we have:

`= (547*434)/(586) =405.116`

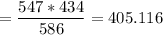
For row 1 column 2 (gloves fit poorly (female)) ; we have:

`= (39*152)/(586) =10.116`

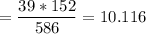
For row 2 column 2 ( gloves fit well ( female ) ; we have:

`= (39*434)/(586) =28.884`

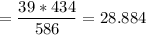
Thus; we can have the complete table to now be:

Observed data Males Females Total

Gloves fit poorly 132 20 152

Gloves fit well 415 19 434

Total 547 39 586

Expected data Males Females Total

Gloves fit poorly 141.884 10.116 152

Gloves fit well 405.116 28.884 434

Total 547 39 586

The Chi - Square Test Statistics can be calculated via the formula:

`X^2 = (\sum (f_o-f_e)^2)/(f_e)`

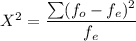
where;

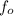`f_o` = observed data frequency

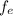`f_e` = expected data frequency

∴

The Chi - Square Test Statistics is as follows:

`=((131-141.884)^2)/(141.884) + ((20-10.116)^2)/(10.116)+ ((415-405.116)^2)/(405.116)+ ((39-28.884)^2)/(28.884)`

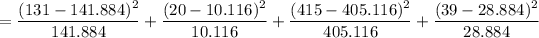
= 0.68+9.6+0.2+3.5

= 13.98

We are given the level of significance ∝ to be = 0.01

numbers of rows = 2; number of column = 2

Thus; the degree of freedom = (2-1)(2-1) = 1×1 = 1

Using the Excel Function : [ = CHISQ.DIST.RT²(X²,df)]

p-value = 0.0002

CONCLUSION: Since the p-value is less than the level of significance ; (i.e p-value < ∝) we reject the null hypothesis and accept the alternative hypothesis.

Thus; there is a difference in the population proportion of glove fitness for the two genders.

Answer 2

Explanation:

Hello!

The objective is to test if the proportion of "X: gloves fitness, categorized: Fit poorly and Fit well" is the same for two populations of interest, "male firefighters" and "female firefighters"

To do this you have to conduct a Chi-Square test of Homogeneity.

In the null hypothesis you have to state that the proportion of the categories of the variable are the same for all the populations of interest.

Be

M: the firefighter is male

F: the firefighter is female

Y: represents the category that the gloves "fit poorly"

W: represents the category that the gloves "fit well"

The null hypothesis will be:

H₀: P(Y|M)=P(Y|F)=P(Y)

P(W|M)=P(W|F)=P(W)

H₁: At least one of the statements in the null hypothesis is false.

α: 0.01

To calculate the statistic under the null hypothesis you have to calculate the expected frequencies first:

`E_(ij)= O_(.j)*(O_(i.))/(n)`

O.j= total of the j-column

Oi.= total of the i-row

n= total of observations

`E_(11)= 547*(152)/(586) = 141.88`

`E_(12)=39*(152)/(586)= 10.12`

`E_(21)= 547*(434)/(586) = 405.12`

`E_(22)= 39*(434)/(586) = 28.88`

`X^2= sum ((O_(ij)-E_(ij))^2)/(E_(ij)) ~~~X^2_((r-1)(c-1))`

r= number of rows (in this case 2)

c=number of columns (in this case 2)

`X^2_(H_0)= ((132-141.88)^2)/(141.88) +((20-10.12)^2)/(10.12) +((415-405.12)^2)/(405.12) +((19-28.88)^2)/(28.88) = 13.95`

Using the critical value approach, you have to remember that this test is always one-tailed to the right, meaning that you'll have only one critical value from which the rejection region is defined:

`X^2_((r-1)(c-1);1-\alpha )= X^2_(1;0.99)= 6.635`

The decision rule is then:

If
`X^2_(H_0)` ≥ 6.635, reject the null hypothesis.

If
`X^2_(H_0)` < 6.635, do not reject the null hypothesis.

The calculated value is greater than the critical value, the decision is to reject the null hypothesis.

So at a 1% level you can conclude that this test is significant. This means that the proportions of gloves fitness, categorized in "Fit poorly" and "Fit well" are different for the male and female firefighters populations.

I hope this helps!