Question

A rocket takes off vertically from the launch pad with no initial velocity but a constant upward acceleration of 2.25 m/s^2. At 15.4 s after blastoff, the engines fail completely so the only force on the rocket from then on is the pull of gravity.

A) What is the max height the rocket will reach above the launch pad?
B) How fast is the rocket moving at the instant before the it crashes onto the launch pad?
C) How long after engine failure does it take for the rocket to crash onto the launch pad?

Answer 1

A) 328 m

B) 80.22 m/s

C) 8.18 sec

Step-by-step explanation:

A)

Initial acceleration of rocket = 2.25 m/s^2

time before engine failure = 15.4 s

initial velocity u of take off = 0 m/s

distance traveled by the rocket under engine power = ?

we'll use Newton's law of motion in this case

S = ut +
`(1)/(2)`a
`t^(2)`

where S is the distance traveled under rocket's acceleration

S = (0 x 15.4) +
`(1)/(2)`(2.25 x
`15.4^(2)`)

S = 0 + 266.81 m = 266.81 m

Final velocity under rocket power before failure will be gotten from,

v = u + at

v = 0 + (2.25 x 15.4) = 34.65 m/s

After the engine failure, the rocket decelerates under gravity at the rate of g = -9.81 m/s^s (acts in downwards direction)

The initial velocity upwards under free deceleration is v = 34.65 m/s

the final velocity will be at the maximum height where rocket stops i.e

u = 0 m/s

the distance covered in this period of free deceleration will be s = ?

using the equation

`v^(2)` =
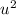`u^(2)` + 2gs

`0^(2)` =
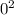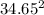`34.65^(2)` + 2(-9.81 x s)

0 = 1200.6 - 19.62s

-1200.6 = -19.62s

s = -1200.6/-19.62 = 61.19 m

therefore,

Maximum Height = 266.81 m + 61.19 m = 328 m

B)

Before descending, at maximum height, the initial velocity of rocket becomes 0 m/s (rocket comes to a stop)

Rocket then descends freely under g = 9.81 m/s^2 (acts in downwards direction)

distance that will be traveled downwards will be 328 m

final velocity v before crashing = ?

using
`v^(2)` =
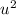`u^(2)` + 2gs

`v^(2)` =
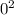`0^(2)` + 2(9.81 x 328)

`v^(2)` = 0 + 6435.36

v =
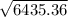`√(6435.36)` = 80.22 m/s

Time taken to reach the pad will be gotten from

v = u + gt

80.22 = 0 + 9.81t

t = 80.22/9.81 = 8.18 sec