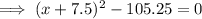Answer:
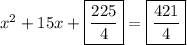

Explanation:
General form of a quadratic equation:

When completing the square, first add the number that is the square of half of
 .
.
Given equation:
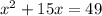
Therefore,
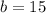
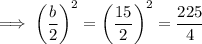
So we need to add 225/4 to both sides of the equation:
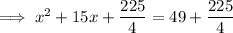

In decimal form:
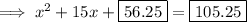
To finish completing the square,
factor the left side of the equation:

Finally, subtract 421/4 from both sides:
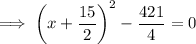
In decimal form: