Answer:
3985 s or 66.42 mins
Step-by-step explanation:
Given:-
- The length of the rod, L = 83.0 cm
- The cross sectional diameter of rod , d = 2.4 cm
- The temperature of reservoir, Tr = 540°C
- The amount of ice in chamber, m = 1.43 kg
- The temperature of ice, Ti = 0°C
- Thermal conductivity of silver, k = 406 W / m.K
- The latent heat of fusion of water, Lf = 3.33 * 10^5 J / kg
Find:-
How much time is required for the ice to melt completely
Solution:-
- We will first determine the amount of heat ( Q ) required to melt 1.43 kg of ice.
- The heat required would be used as latent heat for which we require the latent heat of fusion of ice ( Lf ). We will employ the first law of thermodynamics assuming no heat is lost from the chamber ( perfectly insulated ):
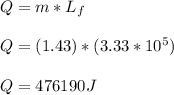
- The heat is supplied from the hot reservoir at the temperature of 540°C by conduction through the silver rod.
- We will assume that the heat transfer through the silver rod is one dimensional i.e along the length ( L ) of the rod.
- We will employ the ( heat equation ) to determine the rate of heat transfer through the rod as follows:
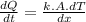
Where,
A: the cross sectional area of the rod
dT: The temperature difference at the two ends of the rod
dx: The differential element along the length of rod ( 1 - D )
t: Time ( s )
- The integrated form of the heat equation is expressed as:
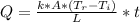
- Plug in the respective parameters in the equation above and solve for time ( t ):

Answer: It would take 66.42 minutes to completely melt the ice