1 Answer

Stefan Wexel · Answer 1 · 2021-06-05T07:38:29+0000

Answer:

The y value achieves its minimum at x = 4/3

Explanation:

Given the graph of y to be 3x² - 8x + 7, to get the value of x for which the graph function achieves its minimum y value, we need to find its turning point first.

At the turning point, dy/dx = 0

Given y = 3x² - 8x + 7

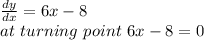
$(dy)/(dx) = 6x-8\\ at\ turning\ point\ 6x-8 = 0$

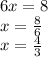
$6x = 8\\x = (8)/(6)\\ x =(4)/(3)$

The y value achieves its minimum at x = 4/3

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

The y value achieves its minimum at x = 4/3

0 Comments

Please log in or register to add a comment.

Other Questions