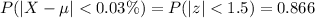Question

Suppose that the raw daily oxygen purities delivered by an air-products supplier have a standard deviation LaTeX: \sigma\approx.1 σ ≈ .1 (percent), and it is plausible to think of daily purites as independent random variables. Approximate the probability that the sample mean LaTeX: \frac{ }{X} X of n = 25 delivered purities falls within .03 (percent) of the raw daily purity mean, LaTeX: \mu μ .

Answer 1

There is a probability of 86.6% that the sample mean falls within 0.03 percent of the raw purity mean.

Explanation:

We have a population standard deviation of σ ≈ 0.1.

We have a sample of size n=25.

Then, we have a sampling distribution, which has a standard deviation for the sample mean that is:

`\sigma_s=(\sigma)/(√(n))=(0.1)/(√(25))=(0.1)/(5)=0.02`

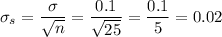
Now, we can calculate a z-score for a deviation of 0.03 percent from the mean as:

`z=(X-\mu)/(\sigma)=(0.03)/(0.02)=(0.03)/(0.02)=1.5`

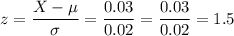
Note: we considered that the margin is ±0.03.

Then, the probability is:

`P(|X-\mu|<0.03\%)=P(|z|<1.5)=0.866`