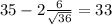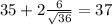Answer:

We know that from the empirical rule we know that within two deviations from the mean we have 95% of the values and if we find the limits we got:
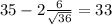
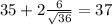
Explanation:
For this case we have the following info given:
 the sample mean
the sample mean
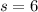 the sample deviation
the sample deviation
 represent the sample mean
represent the sample mean
Since the sample size is higher than 30 we can use the normla approximation and we have this:

We know that from the empirical rule we know that within two deviations from the mean we have 95% of the values and if we find the limits we got: