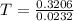Question

Xu owns two investments, A and B, that have a combined total value of $40,000. Investment A is expected to pay $28,000 in 3 years from today and has an expected return of 7.1 percent per year. Investment B is expected to pay $36,000 in T years from today and has an expected return of 5.5 percent per year. What is T, the number of years from today that investment B is expected to pay $36,000?

Answer 1

The number of years is
`T =13 \ years`

Step-by-step explanation:

From the question we are told that

The total value of the investment A and B is
`k =`$40, 000

The future value of A is
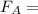`F_A =`$28,000

The time period is t = 3

The expected return of A is
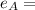`e_A =` 7.1 % = 0.071

The future value of B is
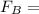`F_B =`$36,000

The time period for B is T

The expected return of B is
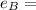`e_B =`5.5 % = 0.055

The present value of investment A is mathematically represented as

`A = (F_A )/((1 + e_A) ^t)`

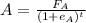
substituting values

`A = ( 28000 )/((1 + 0.071) ^3)`

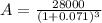
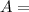`A =`$ 22792.38

The present value of B is mathematically evaluated as

`B = k - A`

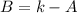
substituting values

B = 40, 000 - 22792.38

B = $17,208

The future value of B is

`F_B = B * (1 + e_B)^T`

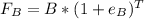
substituting values

`36,000 =17,208 * (1 + 0.055)^T`

`2.0921 = (1.055)^T`

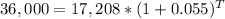
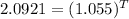
take log of both sides

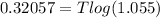
`log(2.0921) =log (1.055)^T`

`0.32057 = T log (1.055)`

=>
`T = (0.3206)/(0.0232)`

`T =13 \ years`