Question

Consider the following set of sample data.

18 26 30 42 50 52 52 76 78 84
For the given data, the mean is_______, the median is________, and the mode is_______.
Suppose the value 76 in the data is mistakenly recorded as 55 instead of 76. For the sample with this error, the mean is_________, the median is______, and the mode is_______. The mean_____, the median_______, and the mode______. Suppose the value 76 in the original sample is inadvertently removed from the sample. For the sample with this value removed, the mean is_______, the median is_______, and the mode is________. The mean_________, the median_______, and the mode________.

Answer 1

For the given data, the mean is 50.8, the median is 51, and the mode is 52.

For the sample with this error, the mean is 48.7, the median is 51, and the mode is 52.

For the sample with this value removed, the mean is 43.2, the median is 50, and the mode is 52.

Explanation:

We are given the following set of sample data below;

18, 26, 30, 42, 50, 52, 52, 76, 78, 84.

The formula for calculating mean is given by;

Mean =
`\frac{\text{Sum of all data values}}{\text{Total number of observations}}`

=
`(18+ 26+ 30+ 42+ 50+ 52+ 52+ 76+ 78+ 84)/(10)`

=
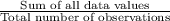
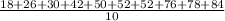
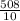`(508)/(10)` = 50.8

For calculating median, we have to observe that the number of observations (n) in our data is even or odd, i.e;

• If n is odd, then the formula for calculating median is given by;

Median =
`((n+1)/(2))^(th) \text{ obs.}`

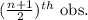
• If n is even, then the formula for calculating median is given by;

Median =
`\frac{((n)/(2))^(th)\text{ obs.} +((n)/(2)+1)^(th)\text{ obs.} }{2}`

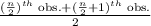
Now, here in our data the number of observations is even, i.e. n = 10.

So, Median =
`\frac{((n)/(2))^(th)\text{ obs.} +((n)/(2)+1)^(th)\text{ obs.} }{2}`

=
`\frac{((10)/(2))^(th)\text{ obs.} +((10)/(2)+1)^(th)\text{ obs.} }{2}`

=
`\frac{5^(th)\text{ obs.} +6^(th)\text{ obs.} }{2}`

=
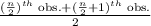
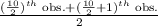
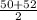`(50+52 )/(2)` = 51

A Mode is a value that appears the maximum number of times in our data.

In our data, the value 52 is appera]ing maximum number of times, i.e. 2 times which means that mode of our data is 52.

Now, suppose the value 76 in the data is mistakenly recorded as 55 instead of 76. For the sample with this error,

• Mean will be changed as value has been changed.

New Mean =
`(18+ 26+ 30+ 42+ 50+ 52+ 52+ 55+ 78+ 84)/(10)`

=
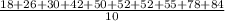
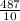`(487)/(10)` = 48.7

• There will be no change in median because there is no change in the 5th and 6th observation of the data.

• Also, there will be no change in mode as stiil 52 appears maximum number of times in our data.

Now, suppose the value 76 in the original sample is inadvertently removed from the sample. For the sample with this value removed,

• Mean will be changed as value has been removed from data.

New Mean =
`(18+ 26+ 30+ 42+ 50+ 52+ 52+ 78+ 84)/(9)`

=
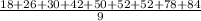
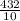`(432)/(10)` = 43.2

• Median will also get changed because the number of observation is now odd, i.e. n = 9

So, Median =
`((n+1)/(2))^(th) \text{ obs.}`

=
`((9+1)/(2))^(th) \text{ obs.}`

=
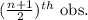
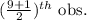
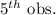`5^(th) \text{ obs.}` = 50

• Also, there will be no change in mode as stiil 52 appears maximum number of times in our data.