Question

The number of tickets purchased by an individual for Beckham College’s holiday music festival is a uniformly distributed random variable ranging from 2 to 10. Find the mean and standard deviation of this random variable. (Round your answers to 2 decimal places.)

Answer 1

The mean of the distribution is 4.00 and the standard deviation is 2.31

Step-by-step explanation:

Given

Range = 2 to 10

Type of distribution = uniform distribution

Required

1. Mean

2. Standard Deviation

The mean of uniform distribution is calculated as thus;

`Mean = (1)/(2)(a + b)`

Where b and a are the intervals of the distribution

b = upper bound = 10

a = lower bound = 2

So,

`Mean = (1)/(2)(a + b)`

Substitute 10 for b and 2 for a

`Mean = (1)/(2)(2 + 10)`

`Mean = (1)/(2)(12)`

`Mean = (1)/(2) * 12`

`Mean = 6`

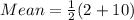
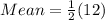
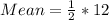
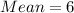
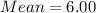`Mean = 6.00` (Approximated to 2 decimal places)

The standard deviation of uniform distribution is calculated as thus;

σ = √σ²

Where σ represents the standard deviation and σ² represents the variance.

Calculate variance

σ² = Var

`Var = ((b-a)^2)/(12)`

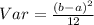
Substitute 10 for b and 2 for a

`Var = ((10 - 2)^2)/(12)`

`Var = (8^2)/(12)`

`Var = (64)/(12)`

`Var = 5.33`

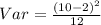
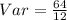
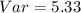
Recall that

σ = √σ² = √Var

Substitute 5.33 for Var

σ = √5.33

σ = 2.309401076758503

σ = 2.31 (Approximated)

Hence, the mean of the distribution is 4.00 and the standard deviation is 2.31