Question

A U.S.-based Internet company offers an online proficiency course in basic accounting. Completing this online course satisfies the "Fundamentals of Accounting" course requirement in many MBA programs. In the first semester, 315 students have enrolled in the course. The marketing research manager divided the country into seven regions of approximately equal population. The course enrollment values for each of the seven regions are given below. The management wants to know if there is equal interest in the course across all regions. Region Enrollment 1 45 2 60 3 30 4 40 5 50 6 55 7 35 The CEO looked at the data presented and said no they are not equal. It is obvious, since the enrollment in one region is 60 and another 30. However, the CFO said that using a Chi-Square Goodness of Fit Test with a 1% significance level, the frequencies in the regions are not significantly different. Which one is correct? Use statistics to support your answer.

Answer 1

`Expected \ mean = (sum \ of \ values )/(n)`

`Expected \ mean = (315 )/(7)`

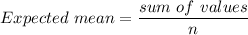
Expected mean = 45

The Chi - Square Value = 15.556

Conclusion:

We conclude that there is equal number of average interest in the course across all regions.

Thus, the CFO is correct, the the frequencies in the regions are not significantly different by using a Chi-Square Goodness of Fit Test with a 1% significance level.

Explanation:

From the question; Let state our null hypothesis and alternative hypothesis

Null Hypothesis

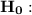`\mathbf{H_0:}`There is equal number of average interest in the course across all regions.

Alternative Hypothesis

`\mathbf{H_a:}` At least one of the region differs in average number of interest in the course.

The table can be better structured as :

Region Enrollment

1 45

2 60

3 30

4 40

5 50

6 55

7 35

From above; we know the number of sample = 7

Then our expected mean can be calculated as :

`Expected \ mean = (sum \ of \ values )/(n)`

`Expected \ mean = (315 )/(7)`

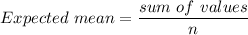
Expected mean = 45

SO, let's construct our Chi-Square Statistics Test Table as follows:

Observed Expected Expected (O-E)²
`((O-E)^2)/(E)`

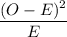
(O) (E) proportion

45 45 0.142857 0 0

60 45 0.142857 225 5

30 45 0.142857 225 5

40 45 0.142857 25 0.556

50 45 0.142857 25 0.556

55 45 0.142857 100 2.222

35 45 0.142857 100 2.222

15.556

The Chi - Square Value = 15.556

Degree of freedom = n- 1

Degree of freedom = 7 - 1

Degree of freedom = 6

Level of significance ∝ = 1% = 0.01

The Critical value of Chi Square test statistic at df = 6 and 0.01 significance level is 16.812

The Decision rule is to reject the Null hypothesis if The Chi Square test statistic X² > 16.812

Thus , since the Chi Square test statistic is lesser than the critical value,

i.e 15.556 < 16.812 ,we accept null hypothesis
`\mathbf{H_0}`

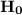
Conclusion:

We conclude that there is equal number of average interest in the course across all regions.

Thus, the CFO is correct, the the frequencies in the regions are not significantly different by using a Chi-Square Goodness of Fit Test with a 1% significance level.