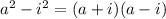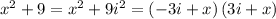Answer:
A. The solutions are
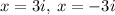 .
.
B. The factored form of the quadratic expression
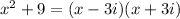
Explanation:
A. To find the solutions to the quadratic equation
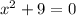 you must:
you must:

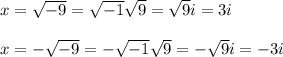
The solutions are:
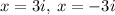
B. Two expressions are equivalent to each other if they represent the same value no matter which values we choose for the variables.
To factor
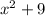 :
:
First, multiply the constant in the polynomial by
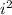 where
where
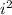 is equal to -1.
is equal to -1.
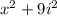
Since both terms are perfect squares, factor using the difference of squares formula