Question

Engineers must consider the breadths of male heads when designing helmets. The company researchers have determined that the population of potential clientele have head breadths that are Normally distributed with a mean of 6.5 inches and a standard deviation of 1.2 inches. According to the 68-95-99.7 rule, we expect 95% of head breadths to be:___________.

Answer 1

"According to the 68-95-99.7 rule, we expect 95% [95.45%] of head breadths to be" between 4.1 inches and 8.9 inches.

Explanation:

According to the 68-95-99.7 rule, approximately:

• 68% (more precisely, 68.27%) of the data from the normal distribution lie one standard deviation,
  `\\ \sigma`, above and below the population mean,
  `\\ \mu`.
• 95% (more precisely, 95.45%) of the data lie two standard deviations,
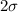  `\\ 2\sigma`, above and below the population mean,
  `\\ \mu`, and finally,
• 99.7 (or more precisely, 99.73%) of the data lie three standard deviations,
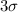  `\\ 3\sigma`, above and below the population mean,
  `\\ \mu`.

Then, if we have--from the question--that:

• The random variable is head breadths.
• This variable follows a normal distribution.
• The population's mean for this distribution is
  `\\ \mu = 6.5` inches.
• The population's standard deviation is
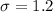  `\\ \sigma =1.2` inches.

We have to remember that two parameters characterize a normal distribution: the population's mean and the population's standard deviation. So, mathematically, the distribution we have from question is
`\\ N(6.5, 1.2)`.

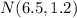For 95% (95.45%) of the head breadths, we expect that they are two standard deviations below and above the population's mean.

For solving this, we need to use the cumulative standard normal distribution (in case we need to find probabilities) and also use standardized values or z-scores:

`\\ z = (x - \mu)/(\sigma)` [1]

A z-score "tells us" the distance from the mean in standard deviations units. If the z-score is positive, it is above the mean. If it is negative, it is below the mean.

Since 95% (95.45%) of the head breadths are two standard deviations (above and below the mean), we have (using [1]):

`\\ \pm2 = (x - \mu)/(\sigma)`

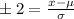
But we already know that
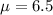`\\ \mu=6.5` inches and
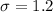`\\ \sigma=1.2` inches.

Thus (without using units) for values above the population's mean:

`\\ 2 = (x - 6.5)/(1.2)`

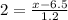
Solving the equation for x, we multiply by 1.2 at each side of [1] :

`\\ 2 * 1.2 = (x - 6.5)/(1.2) * 1.2`

`\\ 2 * 1.2 = (x - 6.5)(1.2)/(1.2)`

`\\ 2 * 1.2 = (x - 6.5)(1.2)/(1.2)`

`\\ 2 * 1.2 = (x - 6.5)*1`

`\\ 2 * 1.2 = x - 6.5`

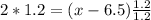
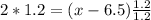
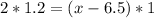
Adding 6.5 at each side of the previous equation:

`\\ (2 * 1.2) + 6.5 = x - 6.5 + 6.5`

`\\ (2 * 1.2) + 6.5 = x + 0`

`\\ (2 * 1.2) + 6.5 = x`

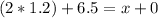
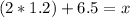
Therefore, the raw value, x, in the distribution that is two standard deviations above the population's mean is:

`\\ x = (2 * 1.2) + 6.5`

`\\ x = 2.4 + 6.5`

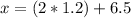
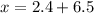
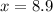`\\ x = 8.9` inches.

For two standard deviations below the mean, we proceed in the same way:

`\\ -2 = (x - 6.5)/(1.2)`

`\\ -2*1.2 = x - 6.5`

`\\ (-2*1.2) + 6.5 = x`

`\\ x = (-2*1.2) + 6.5`

`\\ x = -2.4 + 6.5`

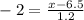
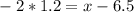
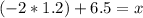
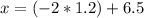
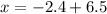
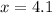`\\ x = 4.1` inches

Therefore, "according to the 68-95-99.7 rule, we expect 95% [95.45%] of head breadths to be" between 4.1 inches and 8.9 inches.

The graph below shows these values, and the shaded area represents 95% of the data, or, to be more precise, 95.45% (0.954499).