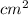Question

In a 30cm by 25cm rectangle, a quadrant of a circle of radius 7cm has been cut away from each corner. What is the perimeter of the part left? and also what is the area of the part left

​

Answer 1

Perimeter = 98 cm

Area = 596
`cm^(2)`

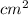
Explanation:

Please refer to the attached image for the resultant figure when a quadrant of circle with radius 7 cm is cut from a rectangle of sides 30 cm and 25 cm.

Perimeter of a figure = Sum of all its sides + Perimeter of circle

Quadrant of a circle is one fourth of a circle and there are 4 such quadrant of a circle, so eventually there is one complete circle in this figure.

The sides of this resultant figure = 30 - 14 = 16 cm

and 25 - 14 = 11 cm

So perimeter of this figure = 16 + 11 + 16 + 11 + Perimeter of circle

`\Rightarrow 54 + 2 \pi r\\\Rightarrow 54 + 2 * (22)/(7) * 7\\\Rightarrow 54 + 44 = 98 cm`

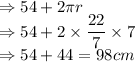
To find area of this figure = Area of rectangle - Area of circle

Area of rectangle = Length
`*` Width

`\Rightarrow 30 * 25 = 750\ cm^(2)`

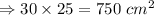
Area of circle =
`\pi r^(2)`

`\Rightarrow (22)/(7) * 7^(2) = 154\ cm^(2)`

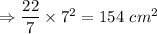
So, area of figure = 750 - 154 = 596
`cm^(2)`