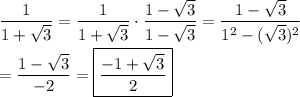Answer:
D. StartFraction negative 1 + StartRoot 3 EndRoot Over 2 EndFraction
Explanation:
Multiply numerator and denominator by the conjugate of the denominator. Then the denominator is the difference of squares, which will be rational. This simplification is called "rationalizing the denominator."