2 Answers

Vuwox · Answer 1 · 2021-06-13T21:49:57+0000

Answer:

Option C.

Explanation:

It is given that

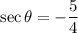
$\sec \theta=-(5)/(4)$

It is also given that
$\theta$ is in second quadrant.

Only sin and coses are positive in second quadrant.

We know that

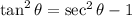
$\tan^2\theta=\sec^2\theta -1$

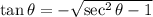$\tan\theta=-√(\sec^2\theta -1)$ [
$\theta$ is in second quadrant]

Substitute
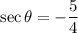$\sec \theta=-(5)/(4)$ in the above equation.

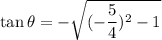
$\tan\theta=-\sqrt{(-(5)/(4))^2 -1}$

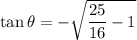
$\tan\theta=-\sqrt{(25)/(16)-1}$

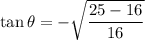
$\tan\theta=-\sqrt{(25-16)/(16)}$

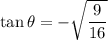
$\tan\theta=-\sqrt{(9)/(16)}$

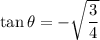$\tan\theta=-\sqrt{(3)/(4)}$ ...(1)

Now, we know that

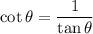
$\cot \theta=(1)/(\tan \theta)$

Using (1), we get

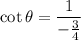
$\cot \theta=(1)/(-(3)/(4))$

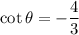
$\cot \theta=-(4)/(3)$

Therefore, the correct option is C.

Please log in or register to add a comment.