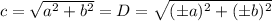Question

What are the similarities in the pythagorean theorem and the distance formula

Answer 1

The Pythagorean theorem states that, for all 90-degree triangles, the relationship between the lengths of the sides is given by the formula a^2 + b^2 = c^2.

DISTANCE FORMULA

The study of geometry in a graphical environment is called co-ordinate geometry.

In co-ordinate geometry, the standard formula for calculating the distance between 2 points is called the distance formula.

Explanation:

Answer 2

Short answer: They are essentially the same thing.

The distance formula is derived from the Pythagorean Theorem

We have distance formula:

`D = √((x_1 - x_2)^2 + (y_1 - y_2)^2)`

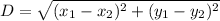
Pythagorean Theorem:

`a^2+b^2=c^2 \Rightarrow c=√(a^2+b^2)`

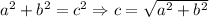
The shortest distance between two points if a line. If you draw a line in the cartesian plane both points will have an x-coordinate and y-coordinate. Note that it forms a right triangle! Therefore, the distance between those points is the hypotenuse.

We can have a point
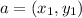`a=(x_(1), y_(1))` and point
`b=(x_(2), y_(2))`

But once
`a` and
`b` can be positive or negative:

`c = √(a^2+b^2)= D = √((\pm a)^2+(\pm b)^2)`