Answer:
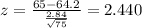
And we can find the probability using the complement rule and with the normal standard table like this:
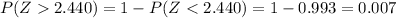
The probability that the mean height for the sample is greater than 65 inches is 0.007
Explanation:
Let X the random variable that represent the women heights of a population, and we know the following parameters
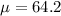 and
and
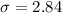
We are interested on this probability
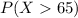
Since the sample size selected is 75>30 we can use the centrel limit theorem and the appropiate formula to use would be the z score given by:

If we find the z score for 65 inches we got:
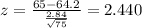
And we can find the probability using the complement rule and with the normal standard table like this:
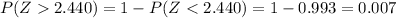
The probability that the mean height for the sample is greater than 65 inches is 0.007