Question

Some of the steps in the derivation of the quadratic formula are shown. Step 3: –c + b^2/4a=a(x^2+b/ax+b^2/4a^2 step4a: -c+b^2/4a=a(x+b/2a)^2 step4b: -4ac/4a+b^2/4a=a(x+b/2a)^2 Which best explains or justifies Step 4b? factoring a polynomial multiplication property of equality converting to a common denominator addition property of equality

Answer 1

C

Explanation:

lol

Answer 2

(C)Converting to a common denominator

Explanation:

Given some of the steps in the derivation of the quadratic formula below:

`\text{Step 3:} -c + (b^2)/(4a)=a(x^2+ (b)/(a)x+ (b^2)/(4a^2))\\\\\text{Step 4a:} -c + (b^2)/(4a)=a(x+(b)/(2a))^2\\\\\text{Step 4b:} (-4ac)/(4a)+ (b^2)/(4a)=a(x+(b)/(2a))^2`

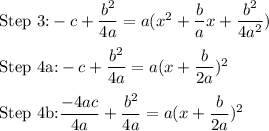
Step 4b is derived from Step 4a by converting the left-hand side to a common denominator 4a.

Therefore, that which best explains or justifies Step 4b is:

(C)Converting to a common denominator