Answer:
C. 1
Explanation:
Given:
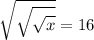
The equation can be rewritten as:
![\displaystyle \large{\sqrt[8]{x} = 16}](https://img.qammunity.org/2023/formulas/mathematics/college/l055u1hvlvzmcj864q10uw2hmgr0fcb1cs.png) via surd property.
via surd property.
Since it’s an even surd, that means there only exists zero-positive numbers for value of x.
To solve this surd equation, simply clear out the surd by powering both sides by 8:
![\displaystyle \large{\left(\sqrt[8]{x}\right )^8=(16)^8}](https://img.qammunity.org/2023/formulas/mathematics/college/nin8hz8bc3blsv1888m2a8rljk2tqbx5cw.png)
Cancel the surd:
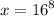
Now, evaluating 16^8 will give up a million and that’s not necessary because we are finding how many solutions this equation has. Since theee only exists one value of x, which is the solution to this equation. Therefore:
Your answer is 1 solution