Answer:
y = -5(x) - 4
Explanation:
Use the equation of a line and substitution.
Information given:
point 1: (-2,6)
x1 = -2 and y1 = 6
point 2: (0,4)
x2 = 0 and y2 = 4
Equation of a line: y = m(x) + b
m = slope
To find slope, you do the equation of a linear slope, which is:
m =
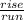 in other words m =
in other words m =
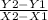
plug in your values

= -5
Great, we've found slope, now to find b
plug in the slope you found: y = -5(x) + b
Plug in and solve for each point given, aka (x,y) into the linear equation for both points.
FIRST POINT:
6 = -5(-2) + b
6 = 10 + b
6 - 10 = b
b = -4
SECOND POINT:
-4 = -5(0) + b
-4 = 0 + b
-4 - 0 = b
b = -4
We got -4 for both, meaning that this equation is correct, so if you add in b, your final equation will be y = -5(x) - 4.
Plug this into desmos.com/calculator, and you'll see this linear equation runs through both points given in the problem.